期望值（Expected Value） 是概率论和统计学中的一个基本概念，用于描述随机变量在大量重复试验中的平均结果。它反映了随机变量的长远趋势，即在多次重复试验中可以期望得到的平均值。

期望值的定义

期望值可以看作是随机变量取值的加权平均数，权重是对应值的概率。具体定义取决于随机变量是离散型还是连续型。

1.离散随机变量的期望值

对于一个离散随机变量 X，它的期望值 E[X]定义为：

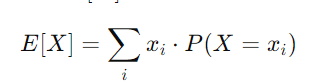
其中：

• xi是随机变量 X 的可能取值，
• P(X=xi)是随机变量取值为 xi的概率。

2.连续随机变量的期望值

对于一个连续随机变量 X，它的期望值 E[X]定义为：

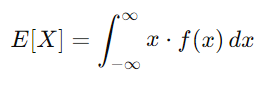
其中：

• f(x) 是随机变量 X的概率密度函数（PDF），
• x是随机变量的取值。

期望值的计算方法

离散随机变量期望值的计算示例

假设你有一个掷骰子的实验，骰子每一面出现的概率都是 1/6。假设随机变量 X表示骰子点数，那么 X的期望值计算如下：

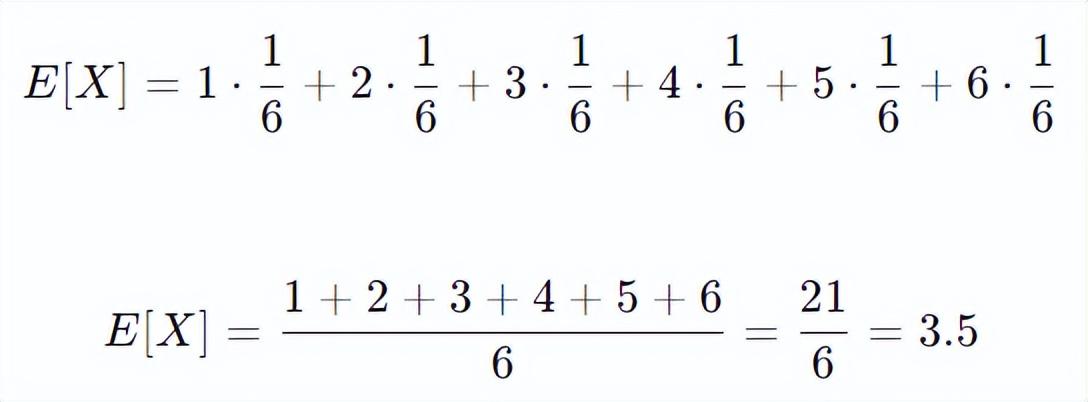
这意味着，如果你重复掷骰子很多次，点数的平均值趋近于 3.5。

连续随机变量期望值的计算示例

假设随机变量 X服从均匀分布在区间 [0, 1] 上，概率密度函数 f(x) 为：

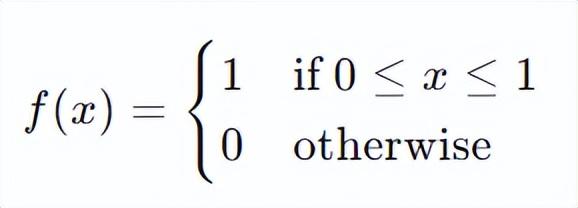
期望值 E[X]E[X]E[X] 的计算如下：

这意味着，在 [0, 1] 区间上均匀分布的随机变量的期望值为 0.5。

期望值的意义

• 平均趋势：期望值表示随机变量在大样本或长时间内的平均结果。
• 决策参考：在决策分析中，期望值常用于比较不同方案的平均收益或风险。